Throughout my scientific career (starting when I first learned about complex systems), it has intrigued me how living systems exploit the richness of dynamics and self-organized patterns which emerge from the entanglement between (biological) cellular processes and physical interactions. I investigate how these complex biological dynamics arise, what purpose they fulfill and how they are maintained and controlled. My current experimental work is carried out in bacterial systems, as they are highly relevant for numerous applications in medicine, industry and ecology and, at the same time, easy to handle in the lab. We combine the rich tool set of synthetic biology (using artificial gene regulatory networks) to control and perturb internal biological dynamics with microfluidic techniques to define precise physico-chemical environments. In parallel, we use nonlinear dynamics, complex systems theory and high-performance computing numerical simulations to study general principles and generate hypotheses. The high degree of control achieved in experiments allows us to connect our theoretical and experimental approaches in order to extract essential ingredients to emergent dynamics, and to use the discovered principles for the design of novel behavior.
Bacterial dynamics & synthetic biology
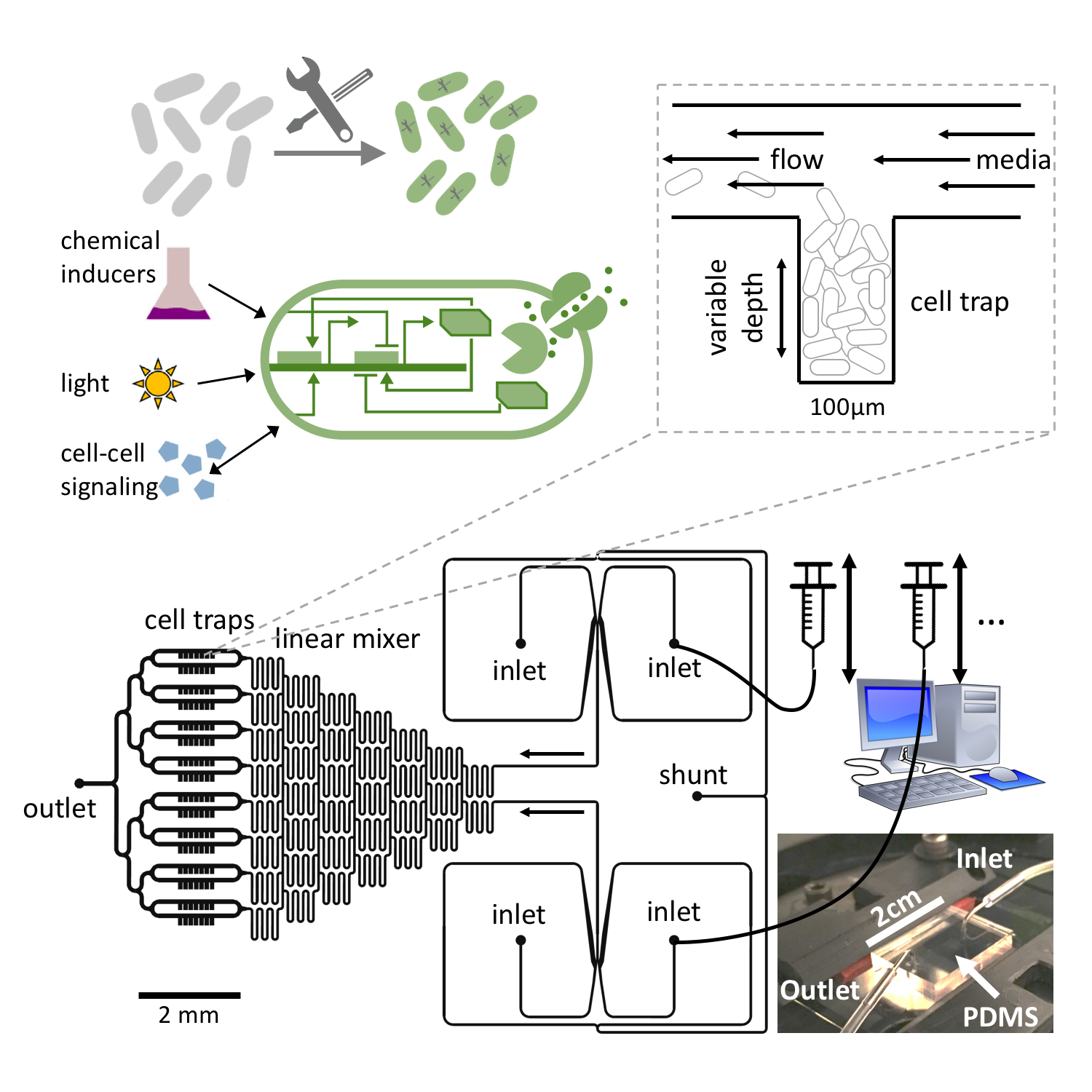
Bacteria like E. coli can be equipped with synthetic gene regulatory networks that either mimic behavior seen elsewhere in nature or provide entirely new functionality. A plethora of synthetic regulatory modules have been developed over the past two decades which enable the construction of more and more complex artificial cellular dynamics (see our recent review). In nature, bacteria exhibit a range of different self-organization phenomena as a result of environmental feedback processes (mechanical interactions, chemical transport, etc) interacting with biological processes such as gene regulation, growth and metabolism. Therefore, the tools of synthetic biology, in conjunction with experimental techniques such as microfluidics, present a unique opportunity to perturb or control both physical and biological ingredients of these complex interactions and study the self-organization of living systems.
One of the most fundamental biological processes is cell growth itself. In a recent publication, we showed how the population dynamics of a bacterial colony can be artificially tuned to different dynamic regimes by gene circuits that use quorum sensing and self-lysis, exploiting the stability properties of the underlying dynamical system which can be derived from a mean field approximation. These properties can then be employed to stabilize otherwise unstable ecologies of multiple bacterial strains.
When bacterial colonies exceeds a certain size, limited diffusion of nutrients and other metabolites leads to the natural emergence of nutrient gradients and heterogeneous growth dynamics (and ultimately cell phenotypes) as cells adapt their metabolism. This represents a prime example of self-organization emerging from the coupling of internal cellular dynamics with physical environmental feedback processes. In our latest preprint, we use microfluidics to create controlled diffusion-limited environments and synthetic gene regulatory modules to modify the response of cells to changing nutrient levels, which lead to a reorganization and dynamic behavior on the population level of microcolonies. In conjunction with a mathematical model, the resulting dynamics point to general stability principles for multi-cellular growth patterns and provide a new strategy to rationally design desired cellular behavior in heterogeneous environments.
Population genetics
How stable are the synthetic circuits that we design inside the host cells in an evolutionary sense? In many cases, it would be advantageous for host cells to deactivate or at least somehow impair a synthetic circuit to lessen the metabolic burden it imposes on the host machinery. In this sense, a random mutation that deactivates a synthetic construct would be a beneficial mutation and so the question arises what factors determine the spread of mutations in bacterial lab populations. Of course, the implications of this research are not limited to synthetic biology, but also apply to, e.g., experimental evolution and directed evolution experiments.
Once a mutation occurs, the mutants can either disappear due to random fluctuations or take over the population. The likelihood of the latter is called the "fixation probability". If mutations arise continuously, this fixation probability also determines the time scale on which one can expect the original genome (or some part thereof, e.g., a synthetic circuit) to be stable before it is replaced with a mutated version. Naturally, more beneficial mutations are more likely to become fixed in the population.
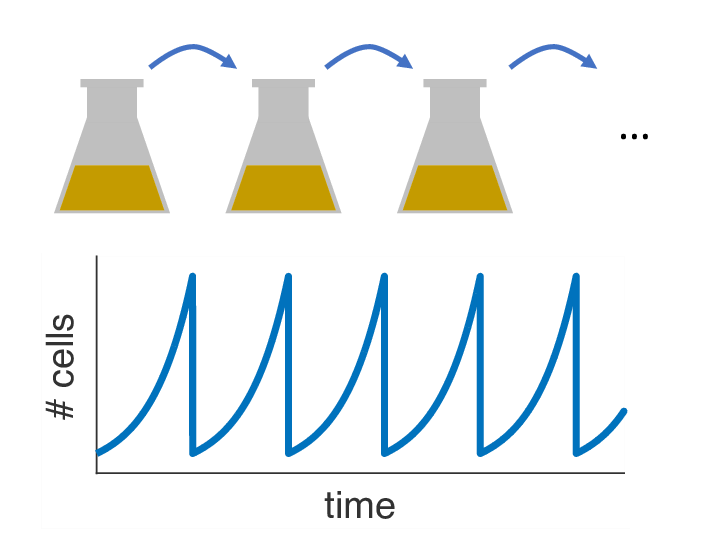
Over the past decades, it has become clear that variations of the population size over time can have a strong influence on the fixation probability as well. In almost any biology lab in the world, there is one particular striking example of externally imposed population size dynamics: the so-called serial passage protocol, where liquid bacterial cultures are periodically diluted into fresh growth media (see picture). As it turns out, this innocent procedure with its seemingly simple dynamics can have complex consequences for the fixation process of beneficial mutations. Read about our recent paper to find out more.
While in the above scenario, the goal would be to limit the impact of mutations as much as possible, experimentalists (and nature itself) often face the converse problem as well: How can evolution be sped up to reach an optimized state of a gene? More specifically, if the optimum lies beyond a deep fitness valley (e.g., if multiple mutations are necessary to confer an advantage, but mutations along the way are detrimental by themselves), how can a population cross this valley in the face of strong selection? Or recent paper proposes a solution based on gene conversion with an inactive duplicate gene and derives analytical estimates for the rates of evolutionary adaptation.
Spiral waves in excitable media

Excitable media are a class of spatially extended systems that support the propagation of non-linear waves that have prominent characteristic properties, such as annihilation of colliding wave fronts (instead of superposition) and refractoriness (the fact the system has to recover before it can be activated in the same spot). Certain chemical reactions (like the famous Belousov-Zhabotinsky reaction) belong to this type of spatio-temporal systems, but biological examples like the emergent aggregation dynamics of the amoeba dictyostelium discoideum are known as well. My interest in excitable media is mostly due to the fact that they also provide a high-level description for the cardiac muscle, where electrical activity is relayed from cell to cell to coordinate the cardiac contraction sequence.
In this abstract picture, plane waves correspond to the regular heart beat where excitation waves emitted by pacemaker cells travel across the heart once to trigger the normal cardiac contraction sequence. However, excitable also support self-sustained activity, most prominently in the form of spiral waves, which correspond to an abnormally increased heart rate as the self-sustained activity in the bulk of the muscle overrides the signal emitted by the (slower) pace makers. Spiral waves can further break up and develop into spatio-temporal chaos consisting of vigorously interacting spiral waves, which corresponds to life-threatening fibrillation in the heart and leads to sudden cardiac death when left untreated.
As spiral waves are thought to be the constitutive elements of many types of arrhythmias, they deserve special attention, and knowledge about their control is key to effectively treating arrhythmias. This is particularly true given the heterogeneity of the cardiac muscle, where spiral waves may pin to non-conducting regions, which stabilizes them and makes them harder to terminate. An important step in the control of these spiral waves therefore is the process of "unpinning". As it turns out, stimulation with electric fields can lead wave emission from the same non-conducting regions, and these induced waves can interact with the pinned wave in such a way as to cause unpinning. First, it is therefore important to understand the mechanisms governing this process and how it compares to other strategies of controlling spiral waves.
Since the success critically depends on the timing of the external stimulus, we then further investigated how reliable unpinning can be achieved with multiple, periodic electric-field pulses. It turns out that the success rate can be surprisingly well predicted with an iterated map that incorporates the phase-response of the pinned spiral to a single electric-field pulse. Due to the stability properties of this map, pacing with a frequency slower than the spiral wave frequency leads to reliable unpinning, while pacing with a higher frequency can lead to phase locking with no chance to unpin the wave. We were recently able to confirm these theoretical predictions in experiments on chicken cardiac muscle cell monolayers. A question that remains is how well these mechanisms translate to the actual situation during a cardiac arrhythmia, where the dynamics is complicated by the 3D structure of the muscle and multiple interacting waves.
Control strategies for cardiac arrhythmias
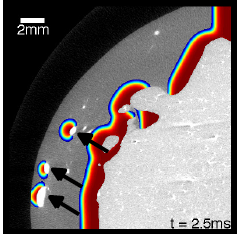
Electric shocks are used in external and implantable defibrillators to terminate life-threatening cardiac arrhythmias such as ventricular fibrillation. Today, these shocks use relatively high energies, sometimes causing intolerable pain (if delivered during consciousness), and potentially further damaging the usually already diseased muscle, although there is conflicting evidence regarding the latter. Therefore, there is a search for low-energy alternatives that use more subtle mechanisms to terminate the spatio-temporal chaos that is thought to underlie fibrillation and restore the heart's normal rhythm. During conventional defibrillation, every single cell is activated, leading to the cessation of all activity due to the tissue's refractoriness. We developed a new method that uses weak pulsed electric fields instead of one big shock and is based on our knowledge about the wave emission caused by the interaction of electric fields with heterogeneities in the tissue (see above). In isolated canine ventricular tissue and in in-vivo experiments on atrial fibrillation, it yields a huge energy reduction, which we believe is due to the presence of heterogeneities throughout the heart and therefore the ability for newly created waves to directly interact with the waves that populate the muscle during fibrillation.
To systematically design such alternative pacing strategies, it is essential to understand how electric fields interact with the complex geometry given by cardiac anatomy. In a theoretical study, we extended the notion of "non-conducting heterogeneity" (cf. above section) to include boundaries of different shapes. It turns out that the local boundary curvature is a major determinant of the sensitivity of the tissue to electric fields, making wave induction at negative curvature boundaries particularly easy. This information can now be used to optimize the electric-field geometry and potentially create adaptive pacing strategies that adjust the number of wave emitting sites in the muscle to the complexity of the arrhythmia.
